A Clean Version of Quick Sort

The core idea of quick sort is choosing a pivot first, then moving those smaller than pivot to its left part and those larger than pivot to its right (partition). Each time we put the pivot at the correct position, so we only need to repeat this procedure to pivot’s left part and right part. This is divide and conquer, which breaks up a larger problem into smaller ones.

My quick sort code before is very ugly and complex, because there are two while loops inside a while loop ! What’s more, I have to think it over and over again each time I use it, since I could’t memorize it. So I decided to make a cleaner version of it. Here is my thinking sharing with you.

Pseudo code for quick sort

1
2
3
4
5
6
7
8
9
10

# Note: stop is not included
def quick_sort(arr, start, stop):
    if there is only 1 element to sort:
        return
    else:
        pivot = choose an element # low or high or randomly
        idx = partition()  # [< pivot | pivot | >= pivot] partition into 3 parts
        quick_sort(left part)  
        quick_sort(right part)
    return

Let me explain it:

1. If there is only 1 element to sort, nothing need to be done, just return the original arr.
2. If ther are more than 1 elements to sort, we need to repeat the procedure below:
   Choose an element as pivot. Pivot is the element which split the to sort array into 3 parts. One is the left part: elements in this part are all < pivot; one is the right part: elements in this part are all >= pivot; the middle part only contains 1 element — the pivot.
   We can assure that, the pivot is at its correct position after such a procedure.
   Now the left part and right part are not sorted yet, so we quick_sort(left part) and right part respectively.

How to write partition ?

For me, the most confusing part of the above algorithm is the partition. Recursion is easy to understand. My old version partition part looks like:

1
2
3
4
5
6
7
8
9
10
11
12

# My old version of partition: Ugly and Hard to understand
low, high = start, stop - 1
pivot = arr[low]
while low <= high:
    while low <= high and arr[low] < pivot:
        low += 1
    if low <= high and arr[low] > pivot:
        arr[low], arr[high] = arr[high], arr[low]
    while high >= low and arr[high] >= pivot:
        high -= 1
    if low <= high and arr[high] < pivot:
        arr[low], arr[high] = arr[high], arr[low]

So how do we make it easier to understand?
Let’s illustrate partition procedure through an example: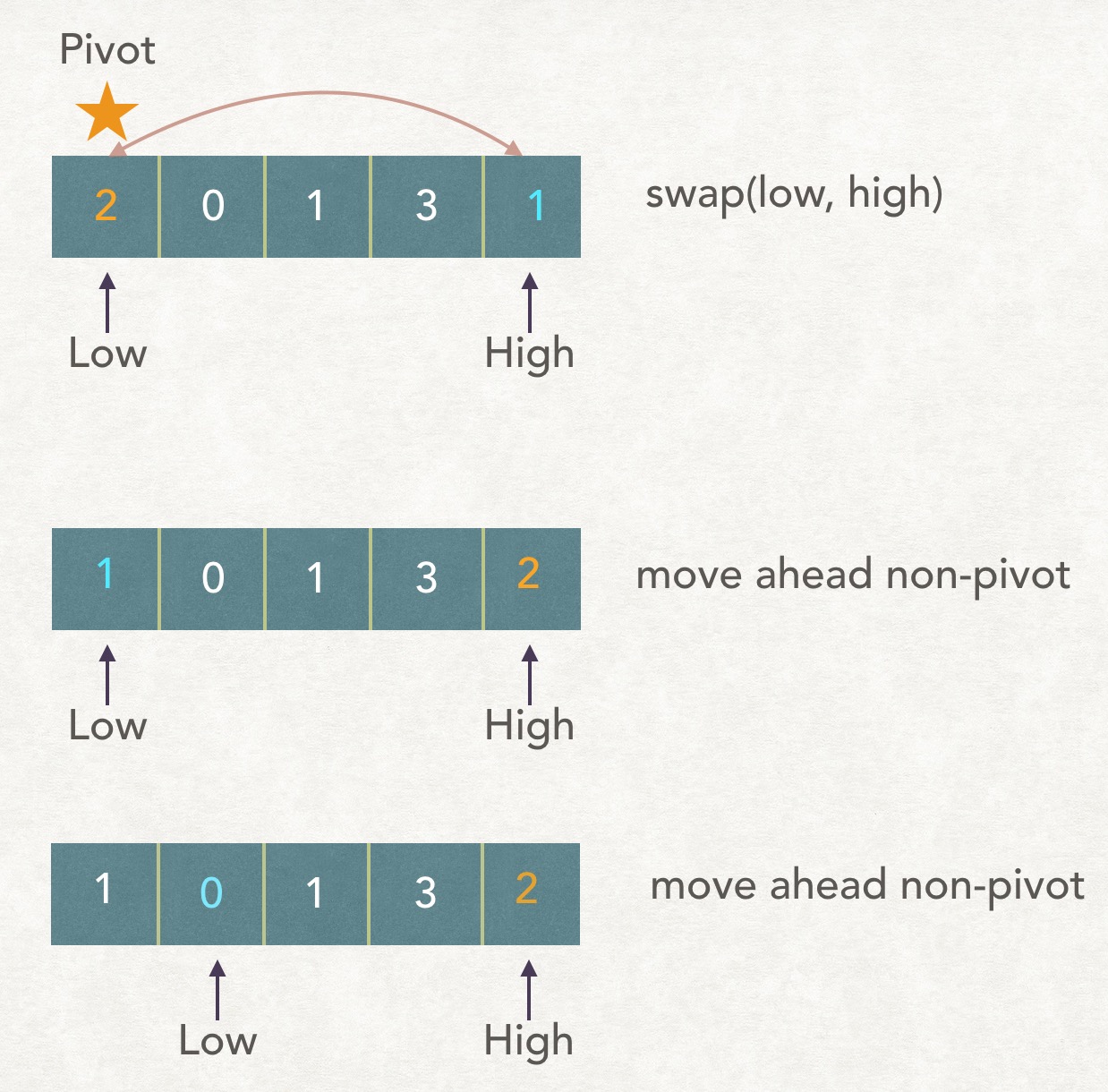

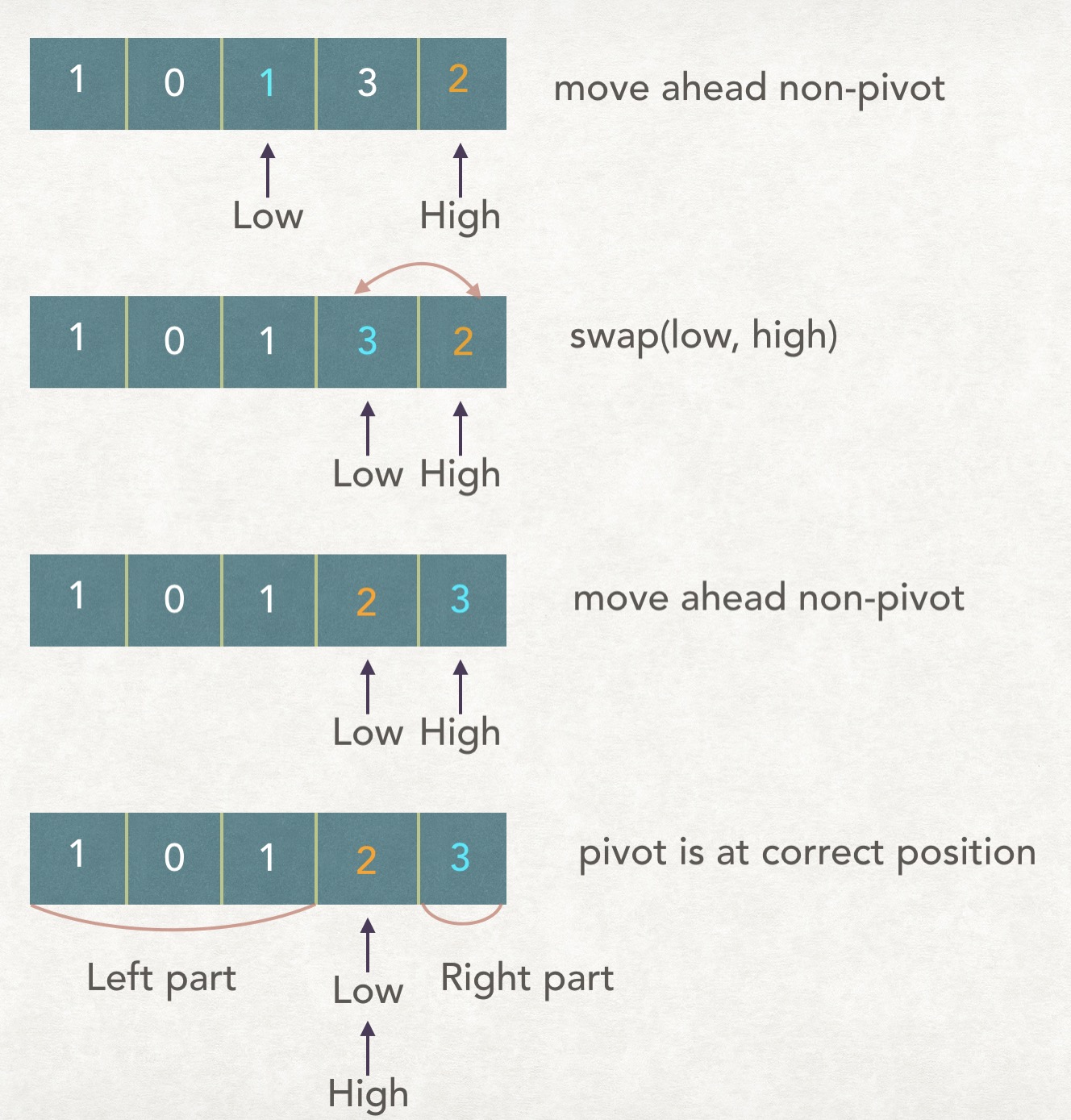
We can find out 4 key points from the above procedure:

1. All swaps only happen between low and high. And pivot must be one of low and high. So swap makes the pivot change its position (Either from low to high or from high to low).
   Note: To remember where is pivot now, I used a variable named pivot to record whether it is at low or high. Note that pivot only has two states: {“low”, “high”}, and swap() will trigger it to change state.
2. When should we make a swap？The answer is: when the low and high are unordered(or in a reversed order).
3. So what if low and high are ordered? The answer is: just move the non-pivot one step forward (low: -->, high: <--).
4. When to stop? The answer is: when the low and high meet together (low == high).

My clean version parition is shown below:

1
2
3
4
5
6
7
8
9
10
11
12
13

LOW = True
HIGH = False
# My new version of partition: Clean and Easy to understand
low, high = start, stop - 1
pivot = LOW
while low < high:
    if arr[low] > arr[high]:  # swap when unordered
        arr[low], arr[high] = arr[high], arr[low]
        pivot = not pivot  # change pivot state
    elif pivot == LOW: # ordered; pivot is LOW
        high -= 1
    else: # ordered; pivot is HIGH
        low += 1

Complete Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

"""
Quick Sort: Divide and Conquer
choose a pivot;
move all eles < pivot into its left and eles > pivvot into its right
Time: Worst case: k == 0 O(N^2), Best & Average case: O(NlogN)
Type: in place, instable
"""
# record the pivot is at low or high
LOW = True
HIGH = False
def quick_sort(arr, start, stop):
    if stop - start <= 1:
        return arr
    low, high = start, stop - 1
    pivot = LOW
    while low < high:
        # swap when unordered
        if arr[low] > arr[high]:
            arr[low], arr[high] = arr[high], arr[low]
            pivot = not pivot
        elif pivot == LOW:
            high -= 1
        else:
            low += 1
    quick_sort(arr, start, low)
    quick_sort(arr, low + 1, stop)  # pivot is already in correct pos, don't sort it!!!
    return arr
if __name__ == "__main__":
    arr = [1, 2, 0, 0, 2, 1, -1, 0, 4, 3]
    # arr = [3, 7, 5, 6, 0, 8, 1, 4]
    # arr = [-1, -2, -3, 1.5, 2.99999, 0.1, 78]
    # arr = [7, 6, 5, 0, 0, 4, 3]
    # arr = [9.2, 8, 7, 5, 3, 20.3, -1, 3.3, 9, 0.3, 0, 2.1, 5, 4.6, 2, 1, 1, 0, 1]
    # arr = [0, 3, 1, 0, -2]
    print("[{}] arr: {}".format(0, arr))
    arr = quick_sort(arr, 0, len(arr))
    print("[{}] arr: {}".format(1, arr))

1
2
3

# output
[0] arr: [1, 2, 0, 0, 2, 1, -1, 0, 4, 3]
[1] arr: [-1, 0, 0, 0, 1, 1, 2, 2, 3, 4]

Note: this version’s quick can only make sure all smaller than pivot nums to its left and all larger nums to its right. It can’t make sure that all nums equal to pivot will lie in one side of pivot.