Bloom Filter

This article will show you what is Bloom Filter (BF for short) and when should we use it. And a python3 implementation of Bloom Filter is shown. Thanks for this article in geeksforgeeks.

What is BF?

Bloom Filter is useful when you want to check whether an element exists in a set. It’s an space-efficient probabilistic data structure, which makes the check quick and only occupies little memory especially when your set is too large to load in memory.
For example, you’re registering a new username, and the server has to check whether your input username is occupied. Since the username set can be very large, so a linear finding algorithm is too slow. And a binary search is also not that efficient. But BF can do it in constant time complexity.

How to build a BF?

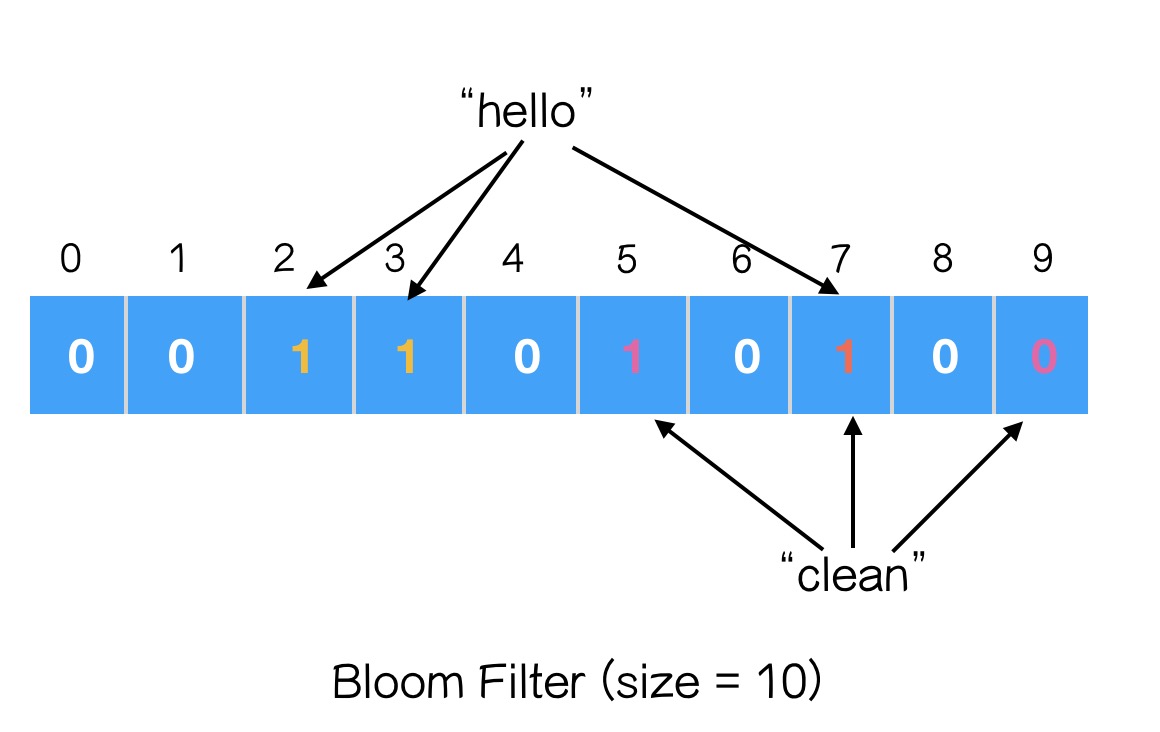
1. Create BF:
   create a bit array with size: N, and initialized with 0s.

2. Add an new element to BF:
   there are k different hash functions: h1(·), h2(·), … hk(·)
   bit_1 = h1(x) % N
   bit_2 = h2(x) % N
   …
   bit_k = hk(x) % N
   and set bit_1, bit_2, … bit_k to 1 in the bit array.

3. Check a element exists in BF:
   repeat step 2: compute bit_1, … bit_k and check whether these bits are all set to 1 in bit array, if Yes then return True.

False Positive Error:
A collision may occur in BF. For example, “near” corresponds to [1,4,5] bits in BF, “going” corresponds to [2,3,5] bits in BF, when we want to check whethe “enjoy” is in BF. We compute the hashes and got [1, 2, 5], we check the BF and found these bits are all 1s, so we return True. But actually “enjoy” is not in our set. This is called False Positive result. e.g. A username is not in the set but BF said it is. And BF will never make False Negative error, that is, telling you an in-set username is not in the set.

Key points to BF:

1. You can lower False Positive rate by taking more space and computing more hash funcs.
2. The hash functions need to be independent and uniformly distributed so that the collision probability won’t be high.
3. Given the set element num $n$ and your expected FP error rate $p$, the Bloom Filter’s array size $m$ and hash functions’s num $k$ can be estimated.
   $$m = -\frac{nlnp}{(ln2)^2}$$
   $$k = \frac{m}{n}ln2$$
4. Given the bf size $m$ and hash function num $k$, the FP rate can be estimated.
   $$p = [1 - (1 - \frac{1}{m})^{kn}]^k \approx (1 - e^{-kn/m})^k $$

Implementation of Bloom Filter:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77

# -*- coding: utf-8 -*-
"""
File: bloom_filter.py
Date: 2018-08-05 18:06
Author: amy
Bloom filter provides a highly efficient way to check whether an item exists in a set.
A False Positive rate is allowed.
Ref: https://www.geeksforgeeks.org/bloom-filters-introduction-and-python-implementation/
"""
import numpy as np
from bitarray import bitarray
from math import ceil
import mmh3
class BloomFilter(object):
    """
    Implement bloom filter.
    """
    def __init__(self, n, fp_prob):
        """
        Create an empty bloom filter.
        Args:
            n: num of the items in set
            fp_prob: false positive prob in tolerance
        """
        self.bit_ary_size = ceil(- n * np.log(fp_prob) / (np.log(2) ** 2))
        self.hash_func_num = ceil(self.bit_ary_size * 1.0 / n * np.log(2))
        self.bit_ary = bitarray(self.bit_ary_size)
        self.bit_ary.setall(0)
        print("Bloom filter size: {}".format(self.bit_ary_size))
        print("Hash func num: {}".format(self.hash_func_num))
    def add(self, item):
        """
        Add an item into set.
        Args:
            item: hashable object
        """
        for i in range(self.hash_func_num):
            set_bit = mmh3.hash(item, i) % self.bit_ary_size
            self.bit_ary[set_bit] = 1
        print("+ {}".format(item))
    def check(self, item):
        """
        Check whether item exists in set.
        Args:
            item: the item to check
        Returns:
            Boolean
        """
        found = True
        for i in range(self.hash_func_num):
            set_bit = mmh3.hash(item, i) % self.bit_ary_size
            if self.bit_ary[set_bit] == 0:
                found = False
                break
        return found
if __name__ == "__main__":
    L = ["hello", "amy", "world", "rainy", "lover", "join", "Go", "plenty"]
    D = ["amy", "go", "rainy", "rain", "love", "Go", "try", "mixed"]
    bf = BloomFilter(len(L), 0.01)
    print("\nBuilding ...")
    for e in L:
        bf.add(e)
    print("\nChecking ...")
    for e in D:
        if bf.check(e):
            print("[{}] existed!".format(e))

Output is:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

Bloom filter size: 77
Hash func num: 7
Building ...
+ hello
+ amy
+ world
+ rainy
+ lover
+ join
+ Go
+ plenty
Checking ...
[amy] existed!
[rainy] existed!
[Go] existed!
## if you enlarge the fp rate, you will find some False Postive results.